什么是椭圆曲线算法？

椭圆曲线算法（Elliptic Curve Cryptography，简称ECC）是一种基于数学理论的密码学技术。与传统的RSA算法相比，椭圆曲线算法在相同安全级别下能使用更短的密钥长度，这就像你用更小的钥匙就能打开更大、更复杂的锁，非常高效和安全。

这种算法的核心在于椭圆曲线方程的性质，通过对这种曲线的点进行运算，可以生成各种密钥和加密信息。这一切都基于现代密码学的数学原理，而这些原理又深深扎根于数论及代数几何中。

椭圆曲线算法如何增强加密货币的安全性？

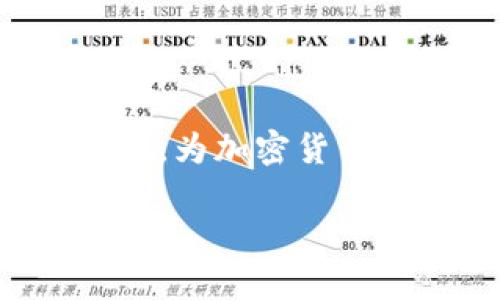
当提到加密货币，大家首先想到的就是比特币、以太坊等数字资产。而使这些资产安全的重要技术，就是我们讨论的椭圆曲线算法。通过使用椭圆曲线算法，用户的私钥和公钥可以在极其安全的环境中生成与储存，极大降低了黑客攻击和盗窃的风险。

例如，比特币使用的就是一种特定的椭圆曲线，即secp256k1。这意味着只要用户妥善管理他们的私钥，即便是对手获得了公钥，也无法反向推出用户的私钥，这样即使数据被截获，攻击者也无法解密出用户的交易信息。

为什么选择椭圆曲线算法？

在加密货币领域，选择椭圆曲线算法的理由有很多：

• 高效性：椭圆曲线算法在计算性能上优于其他形式的加密算法，尤其是在移动设备或者资源受限的设备上，能更快地进行加密与解密操作。
• 安全性：它提供了强大的安全性，相对于相同长度的密钥，ECC能够为用户提供更高的安全防护。
• 密钥管理：更短的密钥长度意味着更便于管理和传输，同时降低了系统资源消耗。

椭圆曲线算法的实际应用

如今，椭圆曲线算法不仅在比特币中得到了应用，很多其他的加密货币如以太坊、瑞波币等也都在利用这一技术以确保用户资产的安全。此外，椭圆曲线算法也在许多领域得到了广泛应用，包括Secure Sockets Layer (SSL)通信、数字签名等。

椭圆曲线算法面临的挑战和未来发展

尽管椭圆曲线算法在加密货币及其他领域表现优越，但仍然面临一些挑战。比如对量子计算的威胁。随着科技进步，未来量子计算机的出现可能会对现有的加密算法构成威胁，业界必须考虑如何改进或者替代现有技术。

此外，用户教育也是提高系统安全性的重要方面。虽然技术的进步能够提升加密算法的安全，用户的不当操作，比如私钥管理不善，仍然是安全事故频发的主要原因。因此，增强用户对加密货币及安全技术的理解至关重要。

相关问题

1. 椭圆曲线算法如何实现高安全性？

椭圆曲线算法实现高安全性的核心在于它的数学基础。椭圆曲线上的点并不是简单的坐标，而是遵循特定的数学规律，这就使得即使对手拥有所有的公钥和加密信息，也几乎不可能反向推导出私钥。这种特性使得椭圆曲线算法在对抗暴力破解和其他类型攻击时，展现出良好的韧性。同时，它的密钥长度相对较短，但安全性并不降低，这使得使用ECC的系统更难以遭受攻击。

2. 为什么加密货币的发展离不开先进的加密技术？

加密货币的发展离不开先进的加密技术，主要因为加密货币本质上依赖于用户的信任和安全保障。如果没有可靠的加密技术支持，用户不敢将资产放在加密货币上，就会对整个市场产生负面影响。例如，几次历史上的重大盗窃事件都表明，弱化的安全协议可以导致用户资产的一夜归零。因此，通过采用椭圆曲线等先进的加密技术，确保交易的安全性不仅是技术选择，更是市场发展的必然要求。

总结

椭圆曲线算法作为一种高效、安全的加密技术，为加密货币的繁荣发展打下了坚实的基础。无论是在技术的设计上，还是在实际应用中，它都展现出强大性能和潜力。然而，面对不断变化的技术环境和市场需求，行业要不断探索，及时跟进安全技术的进步，以确保用户在加密货币投资中的安全和信任。

通过了解椭圆曲线算法的基础知识以及其在加密货币中的应用，我们可以看出，技术发展的背后不仅关乎创新与效率，更涉及到用户的信任与安全。因此，在追寻加密财富的路上，学习与谦逊同样不可或缺。